Coulomb friction, named after Charles-Augustin de Coulomb, is an approximate model used to calculate the force of dry friction. It is governed by the equation:
 is the force of friction exerted by each surface on the other. It is parallel to the surface, in a direction opposite to the net applied force.
is the force of friction exerted by each surface on the other. It is parallel to the surface, in a direction opposite to the net applied force.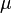 is the coefficient of friction, which is an empirical property of the contacting materials,
is the coefficient of friction, which is an empirical property of the contacting materials, is the normal force exerted by each surface on the other, directed perpendicular (normal) to the surface.
is the normal force exerted by each surface on the other, directed perpendicular (normal) to the surface.
 may take any value from zero up to
may take any value from zero up to 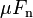 , and the direction of the frictional force against a surface is opposite to the motion that surface would experience in the absence of friction. Thus, in the static case, the frictional force is exactly what it must be in order to prevent motion between the surfaces; it balances the net force tending to cause such motion. In this case, rather than providing an estimate of the actual frictional force, the Coulomb approximation provides a threshold value for this force, above which motion would commence. This maximum force is known as traction.
, and the direction of the frictional force against a surface is opposite to the motion that surface would experience in the absence of friction. Thus, in the static case, the frictional force is exactly what it must be in order to prevent motion between the surfaces; it balances the net force tending to cause such motion. In this case, rather than providing an estimate of the actual frictional force, the Coulomb approximation provides a threshold value for this force, above which motion would commence. This maximum force is known as traction.The force of friction is always exerted in a direction that opposes movement (for kinetic friction) or potential movement (for static friction) between the two surfaces. For example, a curling stone sliding along the ice experiences a kinetic force slowing it down. For an example of potential movement, the drive wheels of an accelerating car experience a frictional force pointing forward; if they did not, the wheels would spin, and the rubber would slide backwards along the pavement. Note that it is not the direction of movement of the vehicle they oppose, it is the direction of (potential) sliding between tire and road.
[edit] The normal force
Main article: Normal force
The normal force is defined as the net force compressing two parallel surfaces together; and its direction is perpendicular to the surfaces. In the simple case of a mass resting on a horizontal surface, the only component of the normal force is the force due to gravity, where 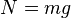 . In this case, the magnitude of the friction force is the product of the mass of the object, the acceleration due to gravity, and the coefficient of friction. However, the coefficient of friction is not a function of mass or volume; it depends only on the material. For instance, a large aluminum block has the same coefficient of friction as a small aluminum block. However, the magnitude of the friction force itself depends on the normal force, and hence the mass of the block.
. In this case, the magnitude of the friction force is the product of the mass of the object, the acceleration due to gravity, and the coefficient of friction. However, the coefficient of friction is not a function of mass or volume; it depends only on the material. For instance, a large aluminum block has the same coefficient of friction as a small aluminum block. However, the magnitude of the friction force itself depends on the normal force, and hence the mass of the block.If an object is on a level surface and the force tending to cause it to slide is horizontal, the normal force
 between the object and the surface is just its weight, which is equal to its mass multiplied by the acceleration due to earth's gravity, g. If the object is on a tilted surface such as an inclined plane, the normal force is less, because less of the force of gravity is perpendicular to the face of the plane. Therefore, the normal force, and ultimately the frictional force, is determined using vector analysis, usually via a free body diagram. Depending on the situation, the calculation of the normal force may include forces other than gravity.
between the object and the surface is just its weight, which is equal to its mass multiplied by the acceleration due to earth's gravity, g. If the object is on a tilted surface such as an inclined plane, the normal force is less, because less of the force of gravity is perpendicular to the face of the plane. Therefore, the normal force, and ultimately the frictional force, is determined using vector analysis, usually via a free body diagram. Depending on the situation, the calculation of the normal force may include forces other than gravity.[edit] Coefficient of friction
The 'coefficient of friction' (COF), also known as a 'frictional coefficient' or 'friction coefficient' and symbolized by the Greek letter µ, is a dimensionless scalar value which describes the ratio of the force of friction between two bodies and the force pressing them together. The coefficient of friction depends on the materials used; for example, ice on steel has a low coefficient of friction, while rubber on pavement has a high coefficient of friction. Coefficients of friction range from near zero to greater than one – under good conditions, a tire on concrete may have a coefficient of friction of 1.7.[citation needed]For surfaces at rest relative to each other
 , where
, where 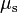 is the coefficient of static friction. This is usually larger than its kinetic counterpart.
is the coefficient of static friction. This is usually larger than its kinetic counterpart.For surfaces in relative motion
 , where
, where 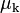 is the coefficient of kinetic friction. The Coulomb friction is equal to
is the coefficient of kinetic friction. The Coulomb friction is equal to  , and the frictional force on each surface is exerted in the direction opposite to its motion relative to the other surface.
, and the frictional force on each surface is exerted in the direction opposite to its motion relative to the other surface.The coefficient of friction is an empirical measurement – it has to be measured experimentally, and cannot be found through calculations. Rougher surfaces tend to have higher effective values. Both static and kinetic coefficients of friction depend on the pair of surfaces in contact; for a given pair of surfaces, the coefficient of static friction is usually larger than that of kinetic friction; in some sets the two coefficients are equal, such as teflon-on-teflon.
Most dry materials in combination have friction coefficient values between 0.3 and 0.6. Values outside this range are rarer, but teflon, for example, can have a coefficient as low as 0.04. A value of zero would mean no friction at all, an elusive property – even magnetic levitation vehicles have drag. Rubber in contact with other surfaces can yield friction coefficients from 1 to 2. Occasionally it is maintained that µ is always < 1, but this is not true. While in most relevant applications µ < 1, a value above 1 merely implies that the force required to slide an object along the surface is greater than the normal force of the surface on the object. For example, silicone rubber or acrylic rubber-coated surfaces have a coefficient of friction that can be substantially larger than 1.
While it is often stated that the COF is a "material property," it is better categorized as a "system property." Unlike true material properties (such as conductivity, dielectric constant, yield strength), the COF for any two materials depends on system variables like temperature, velocity, atmosphere and also what are now popularly described as aging and deaging times; as well as on geometric properties of the interface between the materials. For example, a copper pin sliding against a thick copper plate can have a COF that varies from 0.6 at low speeds (metal sliding against metal) to below 0.2 at high speeds when the copper surface begins to melt due to frictional heating. The latter speed, of course, does not determine the COF uniquely; if the pin diameter is increased so that the frictional heating is removed rapidly, the temperature drops, the pin remains solid and the COF rises to that of a 'low speed' test.[citation needed]
[edit] Approximate coefficients of friction
| Materials | Static friction,  | ||
|---|---|---|---|
| Dry & clean | Lubricated | ||
| Aluminium | Steel | 0.61 | |
| Copper | Steel | 0.53 | |
| Brass | Steel | 0.51 | |
| Cast iron | Copper | 1.05 | |
| Cast iron | Zinc | 0.85 | |
| Concrete (wet) | Rubber | 0.30 | |
| Concrete (dry) | Rubber | 1.0 | |
| Concrete | Wood | 0.62[9] | |
| Copper | Glass | 0.68 | |
| Glass | Glass | 0.94 | |
| Metal | Wood | 0.2–0.6[9] | 0.2 (wet)[9] |
| Polyethene | Steel | 0.2[10] | 0.2[10] |
| Steel | Steel | 0.80[10] | 0.16[10] |
| Steel | PTFE | 0.04[10] | 0.04[10] |
| PTFE | PTFE | 0.04[10] | 0.04[10] |
| Wood | Wood | 0.25–0.5[9] | 0.2 (wet)[9] |
[edit] Static friction
Static friction is friction between two solid objects that are not moving relative to each other. For example, static friction can prevent an object from sliding down a sloped surface. The coefficient of static friction, typically denoted as μs, is usually higher than the coefficient of kinetic friction.The static friction force must be overcome by an applied force before an object can move. The maximum possible friction force between two surfaces before sliding begins is the product of the coefficient of static friction and the normal force:
 . When there is no sliding occurring, the friction force can have any value from zero up to
. When there is no sliding occurring, the friction force can have any value from zero up to 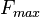 . Any force smaller than
. Any force smaller than 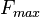 attempting to slide one surface over the other is opposed by a frictional force of equal magnitude and opposite direction. Any force larger than
attempting to slide one surface over the other is opposed by a frictional force of equal magnitude and opposite direction. Any force larger than 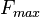 overcomes the force of static friction and causes sliding to occur. The instant sliding occurs, static friction is no longer applicable—the friction between the two surfaces is then called kinetic friction.
overcomes the force of static friction and causes sliding to occur. The instant sliding occurs, static friction is no longer applicable—the friction between the two surfaces is then called kinetic friction.An example of static friction is the force that prevents a car wheel from slipping as it rolls on the ground. Even though the wheel is in motion, the patch of the tire in contact with the ground is stationary relative to the ground, so it is static rather than kinetic friction.
The maximum value of static friction, when motion is impending, is sometimes referred to as limiting friction,[13] although this term is not used universally.[1] It is also known as traction.
[edit] Kinetic friction
Kinetic (or dynamic) friction occurs when two objects are moving relative to each other and rub together (like a sled on the ground). The coefficient of kinetic friction is typically denoted as μk, and is usually less than the coefficient of static friction for the same materials.[14][15] However, Richard Feynman comments that "with dry metals it is very hard to show any difference."[16]New models are beginning to show how kinetic friction can be greater than static friction.[17] Kinetic friction is now understood, in many cases, to be primarily caused by chemical bonding between the surfaces, rather than interlocking asperities;[18]however, in many other cases roughness effects are dominant, for example in rubber to road friction.[17] Surface roughness and contact area, however, do affect kinetic friction for micro- and nano-scale objects where surface area forces dominate inertial forces.[19]
[edit] Angle of friction
For the maximum angle of static friction between granular materials, see Angle of repose.
For certain applications it is more useful to define static friction in terms of the maximum angle before which one of the items will begin sliding. This is called the angle of friction or friction angle. It is defined as:[edit] Friction at the atomic level
Determining the forces required to move atoms past each other is a challenge in designing nanomachines. In 2008 scientists for the first time were able to move a single atom across a surface, and measure the forces required. Using ultrahigh vacuum and nearly-zero temperature (5 K), a modified atomic force microscope was used to drag a cobalt atom, and a carbon monoxide molecule, across surfaces of copper and platinum.[21][edit] Limitations of the Coulomb model
The Coulomb approximation mathematically follows from the assumptions that surfaces are in atomically close contact only over a small fraction of their overall area, that this contact area is proportional to the normal force (until saturation, which takes place when all area is in atomic contact), and that frictional force is proportional to the applied normal force, independently of the contact area (you can see the experiments on friction from Leonardo Da Vinci). Such reasoning aside, however, the approximation is fundamentally an empirical construction. It is a rule of thumb describing the approximate outcome of an extremely complicated physical interaction. The strength of the approximation is its simplicity and versatility – though in general the relationship between normal force and frictional force is not exactly linear (and so the frictional force is not entirely independent of the contact area of the surfaces), the Coulomb approximation is an adequate representation of friction for the analysis of many physical systems.When the surfaces are conjoined, Coulomb friction becomes a very poor approximation (for example, adhesive tape resists sliding even when there is no normal force, or a negative normal force). In this case, the frictional force may depend strongly on the area of contact. Some drag racing tires are adhesive in this way. However, despite the complexity of the fundamental physics behind friction, the relationships are accurate enough to be useful in many applications.
[edit] Numerical simulation of the Coulomb model
Despite being a simplified model of friction, the Coulomb model is useful in many numerical simulation applications such as multibody systems and granular material. Even its most simple expression encapsulates the fundamental effects of sticking and sliding which are required in many applied cases, although specific algorithms have to be designed in order to efficiently numerically integrate mechanical systems with Coulomb friction and bilateral and/or unilateral contact.[22][23] [24] [25] [26] Some quite nonlinear effects, such as the so-called Painlevé paradoxes, may be encountered with Coulomb friction.[27][edit] Fluid friction
Main article: Viscosity
Fluid friction occurs between layers within a fluid that are moving relative to each other. This internal resistance to flow is described by viscosity. In everyday terms viscosity is "thickness". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity. Put simply, the less viscous the fluid is, the greater its ease of movement.All real fluids (except superfluids) have some resistance to stress and therefore are viscous, but a fluid which has no resistance to shear stress is known as an ideal fluid or inviscid fluid.
[edit] Lubricated friction
Main article: Lubrication
Lubricated friction is a case of fluid friction where a fluid separates two solid surfaces. Lubrication is a technique employed to reduce wear of one or both surfaces in close proximity moving relative to each another by interposing a substance called a lubricant between the surfaces.In most cases the applied load is carried by pressure generated within the fluid due to the frictional viscous resistance to motion of the lubricating fluid between the surfaces. Adequate lubrication allows smooth continuous operation of equipment, with only mild wear, and without excessive stresses or seizures at bearings. When lubrication breaks down, metal or other components can rub destructively over each other, causing heat and possibly damage or failure.
[edit] Skin friction
Main article: Parasitic drag
Skin friction arises from the friction of the fluid against the "skin" of the object that is moving through it. Skin friction arises from the interaction between the fluid and the skin of the body, and is directly related to the area of the surface of the body that is in contact with the fluid. Skin friction follows the drag equation and rises with the square of the velocity.Skin friction is caused by viscous drag in the boundary layer around the object. There are two ways to decrease skin friction: the first is to shape the moving body so that smooth flow is possible, like an airfoil. The second method is to decrease the length and cross-section of the moving object as much as is practicable.
[edit] Internal friction
Main article: Plastic deformation of solids
See also: Deformation (engineering)
Internal friction is the force resisting motion between the elements making up a solid material while it undergoes plastic deformation.Plastic deformation in solids is an irreversible change in the internal molecular structure of an object. This change may be due to either (or both) an applied force or a change in temperature. The change of an object's shape is called strain. The force causing it is called stress. Stress does not necessarily cause permanent change. As deformation occurs, internal forces oppose the applied force. If the applied stress is not too large these opposing forces may completely resist the applied force, allowing the object to assume a new equilibrium state and to return to its original shape when the force is removed. This is what is known in the literature as elastic deformation (or elasticity). Larger forces in excess of the elastic limit may cause a permanent (irreversible) deformation of the object. This is what is known as plastic deformation


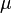 is the coefficient of friction, which is an empirical property of the contacting materials,
is the coefficient of friction, which is an empirical property of the contacting materials, is the
is the 








No comments:
Post a Comment